常用度量

moments：

一阶期望 Expectation
二阶方差 variance，标准差 standard deviation
偏度 Skweness
峰度 Kurtosis, Leptokurtic 尖峰（在方差不变的条件下相应的fat tail）, Platykurtic 低峰

其他：

分位数 quantile
中位数 median
众数 mode

协方差 Covariance

Cov[x, y] = E[(x - E(x)(y - E(y)))] = E[xy] - E[x]E[y] 两种计算方法：

Var(aX + bY) = $a^2 × σ_X^2+ b^2 × σ_Y^2 + 2 ×a ×b× σ_X× σ_Y× ρ_{X,Y}$

Cov(a+bX, c+dY) = bdCov(X, Y)

Corr(a+bX, c+dY) = sign(b)sign(d)Corr(X,Y)

iid 变量的组合

n 个 iid 变量 $x_1 + x_2 + x_3 + … +x_n$

$E = nμ$

$Var = nσ^2$

常用分布

离散分布

PMF probability mass function 概率质量函数，针对离散随机变量

伯努利分布，0/1 分布

E = p ， V = p(1-p)

二项分布 binomial

n 次独立的伯努利随机变量中成功的次数。或者事件发生的概率为p，n 次试验中，事件发生的次数。

$$E = np , V = np(1-p)$$

泊松分布 possion

PMF $$f_Y(x) = \frac{λ^xe^{-λ}}{x!}$$ E = V = λ

λ 的含义是单位时间内事件发生的平均次数。也是波动率大小。要会获得 λ，通常是通过期望，也就是均值。

线性可加

泊松分布的条件：

事件的发生之间独立
发生概率与时间段、或者试验次数 n 成反比

是二项分布 n 很大 p 很小时的一种极限形式。

连续分布

PDF probabiliy density function 概率密度函数，针对连续随机变量

CDF cumulative distribution function 累计分布函数，积分

均匀分布 uniform distribution

正态分布 normal distribution

风险管理中非常常用

特点： $$E = μ$$ $$V = σ^2$$

skew = 0

kurtosis = 3

独立正态分布满足 E、V 的可加性

标准正态分布 $$Z～N(0, 1)$$

标准化方法：$$Z=\frac{(X-μ)}{δ}$$

常用计算： N(-x) = 1 - N(x)

Standardized distance	Central probablity	Central probablity	Critical Value	One-tailed test Test size(α)	Two-tailed test Test size(α)
1δ	68.2%	90%	±1.645	5%	10%
2δ	95.4%	95%	±1.96	2.5%	5%
3δ	99.7%	97.5%(98%)	±2.33	1.25%(1%)	2.5%(2%)
3δ	99.7%	99%	±2.57	0.5%	1%

可以近似代替二项分布（当 np >= 10 且 np(1-p) >= 10）和泊松分布（当λ很大，大于1000）

正态分布的线性组合

中心极限定理

卡方分布

定义为：v 个独立标准正态分布的平方和

假设检验非常重要

level of significance 显著水平

就是 size of test, 就是 α 具体含义解释： 拒绝原假设就是显著，小概率事件不会发生，unlikely to have happened by chance

T 统计 t-statistic

T-value 是什么？就是 t-statistic

公示要记牢 $H_0: μ=μ_0, H_1: μ≠μ_0$ $$T=\frac{\widehatμ-μ_0}{\sqrt{\frac{\widehatσ^2}{n}}}$$

$\sqrt{\widehatσ^2/n}$ 为标准误 standard error

双尾置信 interval $$[\widehat{μ} - C_a× \frac{\widehat{σ}}{\sqrt{n}}, \widehat{μ} + C_a× \frac{\widehat{σ}}{\sqrt{n}}]$$

$$[\bar{X} - z× \frac{s}{\sqrt{n}}, \bar{X} + z ×\frac{s}{\sqrt{n}}]$$

T 分布，t-distribution

critical value

$$C_a$$ 对应正态分布中的 1.64， 1.96 等，需要记忆或查表（结合n和自由度）。

置信区间 confidence interval

two-side
one-side

p-value

p < α，size of test , null reject 计算 p 需要先计算 T value

reject null 判定标准

p-value < α 越小越拒绝
t-static 绝对值 > critical value 越大越拒绝
μ 在置信区间外

Type I vs Type II

一类错误：错杀H0，拒真，test size = α , 显著性水平，significant level 二类错误：错取H0，存伪, β ， power of test

Type II + power of test = 1

一类降低，二类上升；样本容量 n 增加，两者均下降。

power of the test 什么意思？就是 1-β , critical value

卡方分布

多变量

看懂离散多变量概率矩阵

条件分布的计算
条件期望，带权重计算
相关系数在求 E、V 中的使用

正态分布多变量

covariance correlcation coefficient 系数

ordinary least squres 最小二乘法

采样 sample

sample correlation ？

unbias 的 variance: $s^2 = \frac{n}{n-1}σ^2$

$σ=\frac{stdv}{\sqrt{n}}$ 比较模型的有效性，越小越有效。

estimator

mean estimator

$$\widehat{μ}=\frac{\sum_{i=1}^nX_i}{n}$$ $E[\widehat{μ}]=μ$ $V[\widehat{μ}]=\frac{σ^2}{n}$ $SE[\widehat{μ}]=\frac{σ}{\sqrt{n}}$

unbias

BLUE 的特点和含义

unbias 含义：
efficient(best) 含义：在unbias的条件下方差最小
consistent: n 趋向无穷，则采样 $$\bar{μ} \to μ$$

大数定理 LLN

n 非常大时， mean estimator 的 $\widehat{μ}_n$ 趋近于 $μ$

中心极限定理 CLT

是 LLN 的扩展。当 n 非常大，且${X_i}$为 iid，mean 和 variance 都是有限时，$\widehat{μ}$ 的分布趋向于正态分布$N(μ,\frac{σ^2}{n})$ 当 n 增大，variance 在变小。正态分布

$$Z=\frac{\widehat{μ} - μ}{σ/\sqrt{n}}$$

一元线性回归

公式格式： $Y=α + β * X + ε$ $E[T] = α + β E[X]$

计算 estimated slope

$$\widehat{β}=\frac{Cov(X, Y)}{Var(X)}=\frac{Cov(X, Y)}{σ_x^2}=ρ_{xy}\frac{Var(Y)}{Var(X)}=ρ_{xy}\frac{σ_y}{σ_x}$$

dummy 变量

$Y = α + β_1X + β_2(X*D) +ε$

OLS 假设

$σ_{xj}^2 > 0$
残差期望为0
随机变量是 iid
无异方差。每个随机变量不能被其他的随机变量完全解释
没有 outlier。随机变量非完美共线性 perfect colinearity

$R^2$

Coefficient of determination


$ρ$	correlation coefficient
$β$	coefficient
$R^2$	coefficient of determination

TSS：total sum of squre RSS：residual sum of squre ESS: explained sum of squre

ESS + RSS = TSS

$$R^2=\frac{ESS}{TSS}=1-\frac{RSS}{TSS}$$

$$R^2=ρ_{y,x}^2$$

代表数据可被模型解释的比例。

局限性：

增加变量会增大$R^2$
$R^2$ 在不同的变量模型之间无法比较
没有$R^2$ 是好的评判标准

多元线性回归 regression with multiple explanatory variables

$$Y_i=a+β_1Χ_{1i}+β_2Χ_{2i}+…+β_kΧ_{ki}+ε_i$$

partial effect 控制变量 control variable

自由度为独立变量的数量： k

假设

explanatory variable not perfectly linearly dependent 其余与一元线性回归相同。

adjusted R squre

相比 R 方，引入自由度 k。 $$Adjusted\ R^2=1 - [(\frac{n-1}{n-k-1})×\frac{RSS}{TSS}]$$

可能为负

T-test/Z-test

检验一元或多元回归某一回归系数是否为0. 要求：总体分布为正态分布

进行假设$H_0: B_j=B_{j,0} \ 和 \ H_1: B_j≠B_{j,0}$ β_{j,0} 是常数，是总体均值
计算 $$t=\frac{\widehat{β_j}-β_{j,0}}{SE(\widehat{β_j})}$$
比较 t 和 critical value，或者 p-value 与 α

$$\widehat{β_j}$$ 是回归方程中的系数 $β_{j,0}$ 是假设检验中的要检验的系数 $SE(\widehat{β_j})$ 为标准误

如果总体方差已知，则为Z检验，$$SE(\widehat{β_j})=\frac{σ}{\sqrt{n}}$$
如果总体方差未知，则为t检验，$$SE(\widehat{β_j})=\frac{S_n}{\sqrt{n-1}}=\frac{S_{n-1}}{\sqrt{n}}$$

置信区间为$[\widehat{μ} - SE * C_a,\ \widehat{μ} + SE * C_a]$ , $C_a$ 可以查表，查表时注意确定对应的项目，如：n、自由度。

如果是非正态分布，利用中心极限定理，当 n > 30 时，近似的采用 Z 检验或 t 检验

t分布全称是 student’s t 分布。使用场景；小样本 n < 30 df 就是自由度 Degree of freedom 为 n - 1

使用 t 分布时，题目可能会给出对应 t-value 的查表，例如总体方差未知，30次观察，也就是自由度为30-1=29的情况下，置信区间为95%的双尾检验，对应的查表项为t(29, 2.5)

答案为

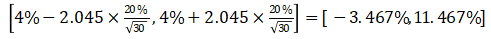
常出现表格题目，给定的t-statistic 和 p-value 的数值都是基于对应的 Ho 假设的 β = 0 的情况，可能不能直接使用。例如:

Chi-square

是检验方差的

F-test

test the model as a whole. 检验多元回归回归系数是否都为0. $$Y_i=a+β_1Χ_{1i}+β_2Χ_{2i}+…+β_kΧ_{ki}+ε_i$$

进行假设 $H_0:β_1=β_2=…β_k=0 和 H1:至少 β_j≠0 \ j\in(1, k)$
计算 $$F=\frac{(TSS-RSS_U)/k}{RSS_U/(n-k-1)}$$

自由度 k，n-k-1

也是看 p-value

不完美多重共线性。

bias-variance tradeoff

遗漏变量和无关变量。

遗漏变量 omitted variable，对Y有贡献且和现有变量有关。会导致包含变量为 bias 和 inconsistent。

无关变量 extraneous included variable 会导致 adjusted R^2 减小。和标准误变大。

小模型：遗漏变量大模型：无关变量

$E[(\widehat{θ}-θ)^2]=Βias^2(\widehat{θ})+Var(\widehat{θ})$

处理方法：

General to Specific，最终达到所有 coefficient 都是统计学显著的
交叉验证 M-fold cross validation，关键词：out-of-sample

Heteroskedasticity

影响有效性，不影响无偏性和一致性。

white 检验

是否存在异方差 Heteroskedasticity

自协方差联合检验 Joint Hypothesis

检验自相关系数是否为0

时间序列

convariance stationary 协方差平稳时间序列

E[Yt] = µ 对于所有 t
方差 variance： $V[Yt] = γ_0 < \infty $ 小于无穷大
协方差： $Cov[Y_t, Y_{t-h}] = γ_h$ 对于所有 t，仅与时间跨度 h 有关

autoconvariance

white noise

均值为0
方差常数且有限
无自相关性

高斯白噪声，残差服从正态分布。

ACF & PACF

ACF 自相关函数，类似相关系数 ρ。值越大，相关性越强。 PACF： partial ACF 多元线性回归后的系数。控制变量，$Y_t$ 和 $Y_{t-τ}$ 的相关性具体含义？

AR & MA & ARMA

AR autoregressive

AR(1) $$Y_t=δ+ΦY_{t-1}+ε_t, ε_t～WN(0, σ^2) $$

均值 $µ = \frac{δ}{(1-Φ)} $
方差 $ γ_0 = \frac{δ^2}{(1-Φ)^2} $
$|φ|<1$，则是协方差平稳， convariance stationary

Lag operator 滞后因子

$$LY_t = Y_{t-1}$$ 计算时，将Y项集中在等号一边，推出包含 (1-L) 的多项式

MA moving average

MA(1) $$Y_t=µ+θε_{t-1}+ε_t, \ ε_t～WN(0, σ^2)$$

均值 µ
方差 $$V[Y_t]=(1+θ^2)σ^2$$

AR ACF decay，PACF cutoff MA 与 AR 相反

ARMA AR + MA

ACF, PACF decay

joint test

联合检验

Box-Pierce 统计卡方
Ljung-Box 统计在小样本表现好

$H_0$: 所有 autocorrelation 系数同时为 0 $H_1$: 至少一个不为零

选取的 h 应当大于ARMA(p, q) 中的 max(p, q)

forcast

H-step-ahead forecast $$\lim_{h\to\infty}\sum_{i=0}^hφ^iδ+φ^hY_Τ= \frac{δ}{(1-φ)}$$ 与 AR(1) 相同。

Non-stationary time seriers

polynomial trend 时间趋势

$$Y_t=δ_ο+δ_1t+ε_t$$ 虽然与 AR 类似，但是 mean 依赖于时间

log-linear 适合固定增长率的时间序列。

seasonality

dummy variables 可用于seasonalities 建模

cycles

除去 time trend 和 season 因素的残差（不包括白噪声），可以使用 AR, MA, ARMA 来构造

random walk

$$Y_t=Y_0+\sum_{i=1}^tε_i$$ 依赖从1到t的每一个shock，每个shock 都会永久影响后续的数值。$V[Y_t]=tσ^2$ 随时间增大而增大。

Unit Root

random walk 是 unit root 的特殊形式。

ADF Augmented Dickey-Fuller test

检验是否 random walk $H_0: γ = 0, \ Η_1: γ < 0$

H-step-ahead forecast

线性时间趋势 $$E[Y{T+h}]=δ_0+δ_1(Τ+h)$$
季节趋势 $$E[Y_{T+h}]=δ+γ_j,\ j=(T+h)(mod\ s),\ γ_0=0$$

Measure return, volatility, correlation

volatility
- daily: $σ_{daily}$
- weekly: $\sqrt{5}σ_{daily}$
- annual: ${\sqrt{252}σ_{daily}}$
return 正态分布检验
Jarque-Bera 检验：就是检验是sknewness 和 kurtosis 否符合正态分布
- $H_0: S = 0\ and\ k = 3$
- $H_1: S ≠ 0\ and\ k ≠ 3$

Linear dependence

Pearson’s correlation, ρ

Non-linear dependence

rank correlation( Spearman’s correlation)
Kendal’s τ(tau)

Kendal tau, Spearman, Pearson correlation non-linear dependence

simulation 仿真

Monte Carlo simulation

局限：
- DGP 依赖
- 计算量大
反复迭代，提高精度
降低 standar error 的方法
- Antithetic variable ，加入另一组与 iid 负相关的随机变量
- Control variable 控制变量

bootstraping

simulation 依赖观测数据去估计 model 参数
bootstraping 直接使用观测数据，不需要对分布进行假设
采样的数据来自于观测数据
iid bootstrapping，replacement（有放回） simple drawing
circular block bootstraping，依赖financial data
局限：
- 市场变化可能导致不可用
- 市场结构会导致与历史数据显著差异

异方差性（ Heteroskedasticity ）：给定解释变量，误差项的方差不为常数。

dependent variable 因变量 independent variable 自变量

error term 残差

计算器手动算各种统计量

multicollinearity vs perfect collinearity

常用度量

协方差 Covariance

iid 变量的组合

常用分布

离散分布

伯努利分布，0/1 分布

二项分布 binomial

泊松分布 possion

连续分布

均匀分布 uniform distribution

正态分布 normal distribution

卡方分布

假设检验 非常重要

level of significance 显著水平

T 统计 t-statistic

T 分布，t-distribution

critical value

置信区间 confidence interval

p-value

reject null 判定标准

Type I vs Type II

卡方分布

多变量

正态分布多变量

采样 sample

estimator

mean estimator

BLUE 的特点和含义

大数定理 LLN

中心极限定理 CLT

一元线性回归

计算 estimated slope

dummy 变量

OLS 假设

$R^2$

多元线性回归 regression with multiple explanatory variables

假设

adjusted R squre

T-test/Z-test

Chi-square

F-test

bias-variance tradeoff

Heteroskedasticity

white 检验

自协方差联合检验 Joint Hypothesis

时间序列

convariance stationary 协方差平稳时间序列

white noise

ACF & PACF

AR & MA & ARMA

AR autoregressive

Lag operator 滞后因子

MA moving average

ARMA AR + MA

joint test

forcast

Non-stationary time seriers

polynomial trend 时间趋势

seasonality

cycles

random walk

Unit Root

ADF Augmented Dickey-Fuller test

H-step-ahead forecast

Measure return, volatility, correlation

Linear dependence

Non-linear dependence

Kendal tau, Spearman, Pearson correlation non-linear dependence

simulation 仿真

Monte Carlo simulation

bootstraping

FEATURED TAGS

假设检验非常重要